Nùmer triangolèr
|
C'l artìcol chè 'l è scrit in
Carpśàn |

Al nùmer triangolèr 'l è 'n nùmer poligonèl ch'al figùra 'n triàngol cumpòst da soquànti unitê mìsi in fila eli ùni atâc a chegli ètri, 'd sóver e 'd sòta, a fèr un triàngol eqvilàter, coi tri cō pèra a 'l só n-éśum post in dla sucesiòun ed tùt i nùmer triangolèr. Con un nùmer intēr n ≥ 1, 'l n-éśum nùmer triangolèr 'l è pèra a la sóma di n nùmer naturêl da 'l 1 a 'l n, psendes aplichèr quèla ch'a s ciàma la "fórmula ed Gauss":
ch'la s pōl anca scrìver c'ma la progresiòun aritmética ed ragiòun 1:
Soquànt nùmer triangolèr i ìn:
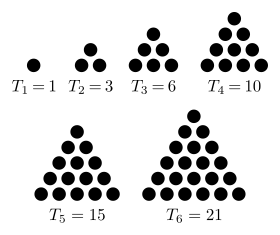
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231,
253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741,
780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431,
1485, 1540, 1596, 1653, 1711, 1770, 1830, 1891, 1953, 2016, 2080 ...[1][2]
Soquànt eśèimpi:
Proprietê
- I nùmer triangolèr i gh'àn dimòndi in cumùn cun chièter nùmer poligonêl, perchè i gh'la chèven sàimper ed fèren na pèrt: la diferèinsa ch'a pasa tra 'l n-éśum nùmer m-gonêl e 'l n-éśum nùmer (m + 1)-gonêl l'è 'l (n − 1)-éśum nùmer triangolèr. P'r eśèimpi, s'a tulòm vìa al quèrt nùmer pentagonêl (22) da 'l quèrt nùmer eśagonêl (28), a s cata al ters nùmer triangolèr, a dir al 6.
- La sóma ed dū nùmer triangolèr ch'i s seguìsen darèint, 'l è 'n nùmer quadrê:
- Al dòpi dl n-éśum nùmer triangulêr 'l è sàimp'r un nùmer oblùng, deśgnènd queschè dala scrìta .
Vóś lighèdi
Noti e referèinsi
- ↑ (EN) 'N elèinc dimòndi gros di nùmer triangolèr in dal sit edl’OEIS.
- ↑ (EN) Sequèinsa OEIS A000217 in dla réda.
Èter progèt
 Wikimedia Commons contiene file multimediali su Nùmer triangolèr
Wikimedia Commons contiene file multimediali su Nùmer triangolèr
Colegamèint estèren
- (EN) Al nùmer triangolèr in dal sit mathworld.com.
- (EN) Na spiegasiòun di nùmer figurê dl'Elena Deza e 'd Michel Deza in PDF, 2011.
- (LA) De institutione arithmetica libri duo dal Boèsi in sìm'a openlibrary.com.






















